这一篇教程,我们继续了解一些内置模块。
四、glob模块
在上一篇教程中,我们通过os模块获取文件夹中的所有文件名,然后组织成多个文件的路径列表,通过fileinput模块进行遍历。
这样的操作比较麻烦。
实际上,我们可以使用glob模块中的函数帮我们简便的实现这个需求。
glob模块支持通配符“*”、“?”、和“[]”,“*”表示0个或多个字符,“?”表示一个字符,“[]”表示匹配指定范围内的字符,例如“[0-9]”匹配数字0-9。
另外,glob模块还支持通配符“**”,能够获取一个目录下所有的目录以及目录中的文件。
glob模块的内容很少,包括3个函数。
- glob(pathname, recursive=False):获取所有匹配路径的列表。参数pathname为需要匹配的路径字符串;参数recursive为递归,调用递归时(值为True),需配合通配符“**”使用,默认为False(不调用递归)。
- iglob(pathname, recursive=False):获取所有匹配路径的生成器,参数同上。
- escape(pathname):忽略所有通配符。
接下来,我们通过glob模块,简化之前的示例代码。
示例代码:
import fileinput,glob
path = r'C:\Users\Administrator\Desktop\song\*.txt' # 设置查询的目标文件夹路径的所有txt文件
files = fileinput.input(glob.glob(path)) # 获取目标文件夹中所有文件
for line in files:
(以下代码省略)
五、heapq模块
heap(堆)是一种数据结构。
普通的队列是顺序排列。
例如:列表[3,2,5,7,1,9,8,6,0,4]进行由小到大的排列就是[0,1,2,3,4,5,6,7,8,9]。
如果我们把这个列表转为带有堆属性的列表(以下简称:堆列表),结果是:[0,1,5,2,3,9,8,6,7,4]
这个堆列表看上去是无序的,实际上是按优先级进行排列。
所以,堆的排列是有规则的排列。
那么,堆的排列规则是怎样的呢?
首先,我们要了解堆的结构,堆是完全二叉树的结构。
列表[3,2,5,7,1,9,8,6,0,4]转换为堆列表时,初始结构如下图:
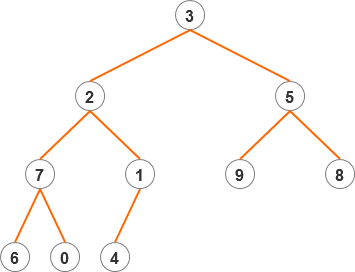
这个结构从上至下,从左至右的获取元素,就是列表中的顺序。
图中的结构,就像倒过来的树(我看更像树根),每一个节点最多有两个分支,所以是完全二叉树的结构。
如果不把这个结构看成树,它也像将多个元素堆在了一起,所以它叫堆。
概念搞清楚,就不会那么迷茫了。
接下来,我们看它是按什么规则重新排序的。
我们堆东西的时候,假设每个物品都有承重上限,为了不把物品压破,我们需要把承重能力小的摆放在上方。
假设列表中的元素数值就是每个元素的承重上限,在已有结构上怎么调整才不会有物品被压破呢?
我们可以按照从下往上,从左往右的顺序进行调整。
每个上层物品和它下层的两个物品比较承重上限,取承重上限最小的放在上层。
也就是说,如果承重最小的物品在下层的话,就和上层的物品位置互换。
那么,在刚才堆的基础之上,我们进行调整,过程如下:
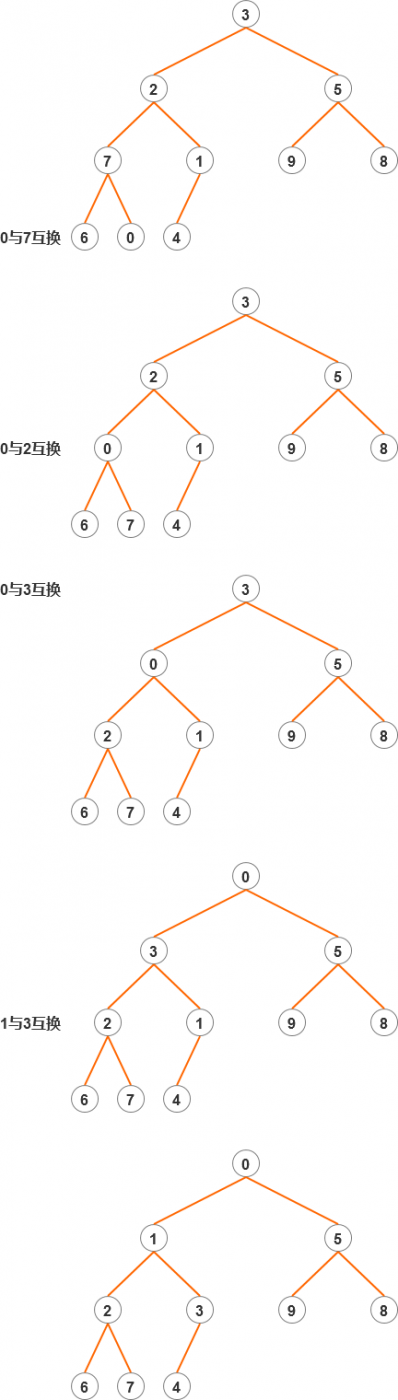
注意,由下至上完成一次调整之后,可能还会存在不符合要求的排列(图中第4步),还要从有问题的位置由下至上继续调整,直到所有排列都符合要求为止。
通过这个调整过程,我们就能够看出堆的排列规则。
这种排列规则可以表示为:heap[index] <= heap[2*index+1] and heap[index] <= heap[2*index+2]
也就是每一个父节点的数值小于等于两个子节点的数值。
因为,堆的这种优先规则,在获取一个列表的最小值时(可以增加元素的同时找到最小元素),要比列表的min()函数更加快捷。
Python中没有独立的堆类型,只是在内置模块heapq中提供了一些操作堆的函数。
heapify(list):将列表转换堆列表。
heappush(heap,item):执行将元素入堆的操作,heap为已有堆列表,item为新的入堆元素。
heappop(heap):取出堆中最小元素。
heapreplace(heap,item):替换堆列表中最小的元素为新元素。
heappushpop(heap,item):新元素入堆,然后取出堆列表中最小的元素。
nlargest(n, iterable, key=None):获取最大的n个元素。
nsmallest(n, iterable, key=None):获取最小的n个元素。
merge(*iterables):将多个列表合并,并进行堆调整,返回的是合并后的列表的迭代器。
接下来,通过示例代码演示上方函数的使用方法。
示例代码:
import heapq # 导入需要使用的模块 heap = [3, 2, 5, 7, 1, 9, 8, 6, 0, 4] heapq.heapify(heap) # 列表转换为堆列表 print(heap) # 显示输出结果为:[0, 1, 5, 2, 3, 9, 8, 6, 7, 4] heapq.heappush(heap, 0.5) # 新元素入堆 print(heap) # 显示输出结果为:[0, 0.5, 5, 2, 1, 9, 8, 6, 7, 4, 3] print(heapq.heappop(heap)) # 取出堆列表中最小的元素,显示输出结果为:0 print(heap) # 显示输出结果为:[0.5, 1, 5, 2, 3, 9, 8, 6, 7, 4] heapq.heapreplace(heap, 10) # 替换堆列表中最小的元素为新元素 print(heap) # 显示输出结果为:[1, 2, 5, 6, 3, 9, 8, 10, 7, 4] print(heapq.heappushpop(heap, 11)) # 新元素入堆,然后取出堆列表中最小的元素,显示输出结果为:1 print(heap) # 显示输出结果为:[2, 3, 5, 6, 4, 9, 8, 10, 7, 11] print(heapq.nlargest(5, heap)) # 显示输出结果为:[11, 10, 9, 8, 7] print(heapq.nsmallest(5, heap)) # 显示输出结果为:[2, 3, 4, 5, 6] print(list(heapq.merge([1, 4, 7], [0, 2, 5]))) # 显示输出结果为:[0, 1, 2, 4, 5, 7]
本节知识点:
1、glob模块
2、堆的结构
3、heapq模块
本节英文单词与中文释义:
1、glob:一团
2、recursive:递归
3、escape:规避
4、heap:堆
5、heapq(heap queue):堆队列
6、ify:动词后缀,表示使……化
7、push:增加
8、largest:最大的
9、smallest:最小的
10、merge:合并
转载请注明:魔力Python » Python3萌新入门笔记(39)